
REVSTAT – Statistical Journal
Volume 16, Number 2, April 2018, 187–212
MODIFIED SYSTEMATIC SAMPLING WITH
MULTIPLE RANDOM STARTS
Authors: Sat Gupta
– Department of Mathematics and Statistics, University of North Carolina,
Greensboro, USA
sngupta@uncg.edu
Zaheen Khan
– Department of Mathematics and Statistics, Federal Urdu University
of Arts, Science and Technology, Islamabad, Pakistan
zkurdu@gmail.com
Javid Shabbir
– Department of Statistics, Quaid-i-Azam University,
Islamabad, Pakistan
javidshabbir@gmail.com
Received: February 2017 Revised: July 2017 Accepted: August 2017
Abstract:
• Systematic sampling has been facing two problems since its beginning; situational
complications, e.g., population size N not being a multiple of the sample size n, and
unavailability of unbiased estimators of population variance for all possible combi-
nations of N and n. These problems demand a sampling design that may solve the
said problems in a practicable way. In this paper, therefore, a new sampling design
is introduced and named as, “Modified Systematic Sampling with Multiple Random
Starts”. Linear systematic sampling and simple random sampling are the two extreme
cases of the proposed design. The proposed design is analyzed in detail and various
expressions have been derived. It is found that the expressions for linear system-
atic sampling and simple random sampling may be extracted from these expressions.
Finally, a detailed efficiency comparison is also carried out in this paper.
Key-Words:
• Modified Systematic Sampling; Linea r Systematic Sampling; Simple Random Sam-
pling; Circular Systematic Sampling; Modified Systematic Sampling: Linear Trend.
AMS Subject Classification:
• 62DO5.
188 Sat Gupta, Zaheen Khan and Javid Shabbir

Modified Systematic Sampling with Multiple Random Starts 189
1. INTRODUCTION
Systematic sampling is generally more efficient than Simple Random Sam-
pling (SRS) because SRS may include bulk of units from high density or low
density parts of the region, whereas the systematic sampling ensures even cover-
age of the entire region for all units. In many situations, systematic sampling is
also more precise than stratified random sampling. Due to this, researchers and
field workers are often inclined towards systematic sampling.
On the other hand, in Linear Systematic Sampling (LSS), we may obtain
sample sizes that vary when the population size N is not a multiple of the sample
size n, i.e., N 6= nk, where k is the sampling interval. However, this problem can
be dealt by Circular Systematic Sampling (CSS), Modified Systematic Sampling
(MSS) proposed by Khan et al. (2013), Remainder Linear Systematic Sampling
(RLSS) proposed by Chang and Huang (2000) and Generalized Modified Lin-
ear Systematic Sampling Scheme (GMLSS) proposed by Subramani and Gupta
(2014). Another well-known and long-standing problem in systematic sampling
design is an absence of a design based variance estimator that is theoretically
justified and generally applicable. The main reason behind this problem lies
in the second-order inclusion probabilities which are not p ositive for all pairs
of units under systematic sampling scheme. It is also obvious that population
variance can be unbiasedly estimated if and only if the second-order inclusion
probabilities are positive for all pairs of units. To overcome this problem, several
alternatives have been proposed by different researchers. However, the simplest
one is the use of multiple random starts in systematic sampling. This procedure
was adopted by Gautschi (1957) in case of LSS. Later on, Sampath (2009) has
considered LSS with two random starts and develop ed an unbiased estimator
for finite-population variance. Sampath and Ammani (2012) further studied the
other versions (balanced and centered systematic sampling schemes) of LSS for
estimating the finite-population variance. They also discussed the question of
determination of the number of random starts. Besides these attempts, the other
approaches proposed by different researchers in the past are not much beneficial
due to the considerable loss of simplicity.
From the attempts of Gautschi (1957), Sampath (2009), Sampath and Am-
mani (2012) and Naidoo et al. (2016), unbiased estimation of population variance
becomes possible just for the case in which N = nk. Therefore, to avoid the diffi-
culty in estimation of population variance for the case N 6= nk, practitioners are
unwillingly inclined towards SRS instead of sy stematic sampling. Such limita-
tions demand a more generalized sampling design which can play wide-ranging
role in the theory of systematic sampling. Thus, in this paper we propose Modi-
fied Systematic Sampling with Multiple Random Starts (MSSM). The MSSM en-
sures unbiased estimation of population variance for the situation where N 6= nk.
190 Sat Gupta, Zaheen Khan and Javid Shabbir
As one can see, MSS proposed by Khan et al. (2013) nicely arranges the popula-
tion units into k
1
systematic groups each containing s number of units. In MSS,
initially a group is selected at random and other (m − 1) groups are systemat-
ically selected. In this way, a sample of size n consisting of m groups of size s
is achieved. Whereas in MSSM, we propose to select all m systematic groups at
random to get a sample of size n. Such selection enables us to derive the unbiased
variance estimator in systematic sampling. It is interesting to note that LSS and
SRS become the extreme cases of MSSM. The MSSM becomes LSS in a situation
when N itself is the least common multiple (lcm) of N and n or equivalently
N = nk, and becomes SRS if lcm is the product of N and n. Because in the
case when N = nk we are selecting m = 1 group at random which resembles LSS.
Whereas, if lcm is the product of N and n we have N groups each containing
only one unit from which we are selecting n groups at random in MSSM, which
is similar to SRS. In case of LSS, variance estimation can be easily dealt with
by Gautschi (1957), Sampath (2009), Sampath and Ammani (2012) and Naidoo
et al. (2016); whereas the worst case of MSSM is SRS, where unbiased variance
estimation can be done using SRS approach.
2. MODIFIED SYSTEMATIC SAMPLING WITH MULTIPLE
RANDOM STARTS
Suppose, we have a population of size N, the units of which are denoted
by {U
1
, U
2
, U
3
, ..., U
N
}. To select a sample of size n from this population, we will
arrange N units into k
1
= L/n (where L is the least common multiple of N and n)
groups, each containing s = N/k
1
elements. The partitioning of groups is shown
in Table 1. A set of m = L/N groups from these k
1
groups are selected using
simple random sampling without replacement to get a sample of size ms = n.
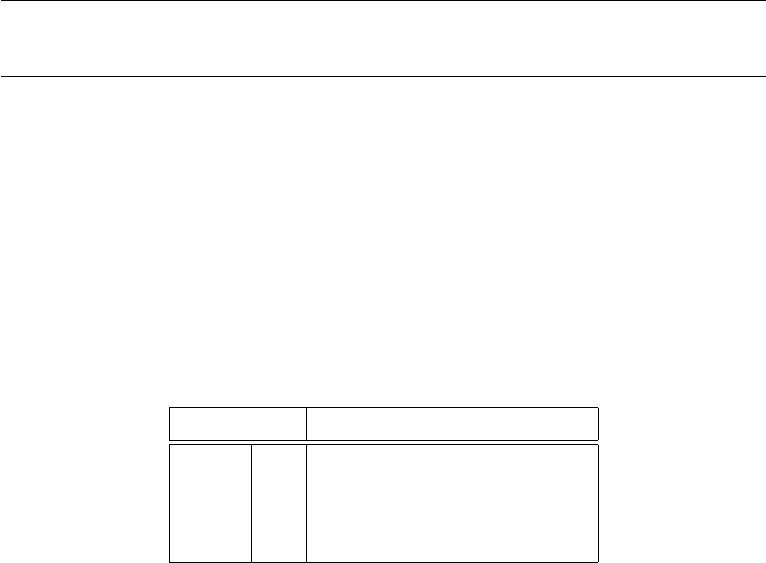
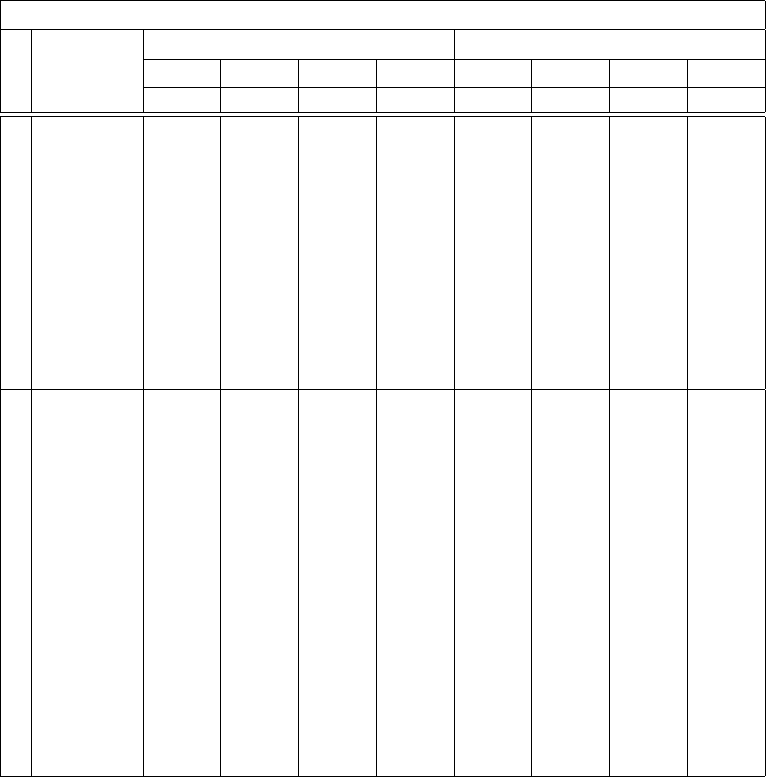
Table 1: Labels of population units arranged in MSSM.
Lab els of Sample units
G
1
U
1
U
k
1
+1
. . U
(s−1)k
1
+1
G
2
U
2
U
k
1
+2
. . U
(s−1)k
1
+2
Groups G
3
U
3
U
k
1
+3
. . U
(s−1)k
1
+3
G
i
U
i
U
k
1
+i
. . U
(s−1)k
1
+i
G
k
1
U
k
1
U
2k
1
. . U
sk
1
=N
Thus sample units with random starts r
i
(i = 1, 2, ..., m) selected from 1 to
k
1
correspond to the following labels:
(2.1) r
i
+ (j − 1)k
1
, i = 1, 2, ..., m and j = 1, 2, ..., s.

Modified Systematic Sampling with Multiple Random Starts 191
2.1. Estimation of Population Mean and its Variance in MSSM
Consider the mean estimator
¯y
MSSM
=
1
ms
m
X
i=1
s
X
j=1
y
r
i
j
=
1
m
m
X
i=1
1
s
s
X
j=1
y
r
i
j
.
where y
r
i
j
is the value of the jth unit of the ith random group.
Taking expectation on both sides, we get:
E (¯y
MSSM
) =
1
m
m
X
i=1
E
1
s
s
X
j=1
y
r
i
j
=
1
m
m
X
i=1
1
k
1
k
1
X
i=1
1
s
s
X
j=1
y
ij
=
1
sk
1
k
1
X
i=1
s
X
j=1
y
ij
= µ,
where y
ij
is the value of the jth unit of the ith group and µ is the population
mean.
The variance of ¯y
MSSM
is given by
V (¯y
MSSM
) = E (¯y
MSSM
− µ)
2
=
1
m
2
E
m
X
i=1
(¯y
r
i
.
− µ)
2
,
where ¯y
r
i
.
is the mean of ith random group.
After simplification, we have:
(2.2) V (¯y
MSSM
) =
1
mk
1
(k
1
− m)
(k
1
− 1)
k
1
X
i=1
(¯y
i.
− µ)
2
,
where ¯y
i.
is the mean of ith group.
Further, it can be observed that in a situation when MSSM becomes LSS,
the variance expression given in Equation (2.2) reduces to variance of LSS, i.e.,
V (¯y
MSSM
) =
1
k
k
X
i=1
¯y
i.
− µ
2
= V (¯y
LSS
).
Similarly, in the case when MSSM becomes SRS, V (¯y
MSSM
) reduces to
variance of SRS without replacement, i.e.,
V (¯y
MSSM
) =
(N − n)
nN
1
(N − 1)
N
X
i=1
y
i
− µ
2
= V (¯y
SRSW OR
) .
The alternative expressions for V (¯y
MSSM
) have been presented in Theo-
rems 2.1, 2.2 and 2.3:
192 Sat Gupta, Zaheen Khan and Javid Shabbir
Theorem 2.1. The variance of sample mean under MSSM is:
V (¯y
MSSM
) =
1
mN
(k
1
− m)
(k
1
− 1)
h
(N − 1)S
2
− k
1
(s − 1)S
2
wg
i
,
where S
2
=
1
N − 1
k
1
X
i=1
s
X
j=1
(y
ij
− µ)
2
, and S
2
wg
=
1
k
1
(s − 1)
k
1
X
i=1
s
X
j=1
(y
ij
− ¯y
i
)
2
is
the variance among the units that lie within the same group.
Proof: From analysis of variance, we have:
N
X
i=1
(y
i
− µ)
2
= s
k
1
X
i=1
(¯y
i
− µ)
2
+
k
1
X
i=1
s
X
j=1
(y
ij
− ¯y
i
)
2
, or
(N − 1)S
2
= s
k
1
X
i=1
(¯y
i
− µ)
2
+ k
1
(s − 1)S
2
wg
.
Thus
(2.3) V (¯y
MSSM
) =
1
mN
(k
1
− m)
(k
1
− 1)
h
(N − 1)S
2
− k
1
(s − 1)S
2
wg
i
.
Theorem 2.2. The variance of sample mean under MSSM is:
V (¯y
MSSM
) =
1
n
k
1
− m
k
1
− 1
N − 1
N
S
2
h
1 + (s − 1)ρ
w
i
,
where
ρ
w
=
k
1
P
i=1
s
P
j=1
s
P
j
′
=1
j
′
6=j
(y
ij
− µ)(y
ij
′
− µ)/s(s − 1)k
1
k
1
P
i=1
s
P
j=1
(y
ij
− µ)
2
/sk
1
.
Proof: Note that
V (¯y
MSSM
) =
1
mk
1
(k
1
− m)
(k
1
− 1)
k
1
X
i=1
(¯y
i
− µ)
2
=
1
s
2
mk
1
(k
1
− m)
(k
1
− 1)
k
1
X
i=1
h
s
X
j=1
(y
ij
− µ)
i
2
=
1
s
2
mk
1
(k
1
− m)
(k
1
− 1)
h
k
1
X
i=1
s
X
j=1
(y
ij
− µ)
2
+
k
1
X
i=1
s
X
j6=1
(y
ij
− µ)(y
iu
− µ)
i
=
1
s
2
mk
1
(k
1
− m)
(k
1
− 1)
h
(sk
1
− 1)S
2
+ (sk
1
− 1)(s − 1)S
2
ρ
w
i
.

Modified Systematic Sampling with Multiple Random Starts 193
Hence
(2.4) V (¯y
MSSM
) =
1
n
(k
1
− m)
(k
1
− 1)
(N − 1)
N
S
2
h
1 + (s − 1)ρ
w
i
,
where ρ
w
is the intraclass correlation between the pairs of units that are in the
same group.
Theorem 2.3. The variance of ¯y
MSSM
is:
V (¯y
MSSM
) =
(k
1
− m)
mN
S
2
wst
h
1 + (s − 1)ρ
wst
i
,
where
S
2
wst
=
1
s(k
1
− 1)
s
X
j=1
k
1
X
i=1
(y
ij
− ¯y
.j
)
2
and
ρ
wst
=
k
1
P
i=1
s
P
j=1
s
P
j
′
=1
j
′
6=j
(y
ij
− ¯y
j
) (y
ij
′
− ¯y
j
′
)
s(s − 1) (k
1
− 1)S
2
wst
.
Proof: Note that
V (¯y
MSSM
) =
1
mk
1
(k
1
− m)
(k
1
− 1)
k
1
X
i=1
(¯y
i
− µ)
2
=
1
mk
1
(k
1
− m)
(k
1
− 1)
k
1
X
i=1
h
1
s
s
X
j=1
y
ij
−
1
s
s
X
j=1
¯y
j
i
2
=
1
s
2
mk
1
(k
1
− m)
(k
1
− 1)
k
1
X
i=1
h
s
X
j=1
(y
ij
− ¯y
j
)
i
2
=
1
smN
(k
1
− m)
(k
1
− 1)
"
s
X
j=1
k
1
X
i=1
(y
ij
− ¯y
j
)
2
+
k
1
X
i=1
s
X
j=1
s
X
j
′
=1
j
′
6=j
(y
ij
− ¯y
j
)(y
ij
′
− ¯y
j
′
)
#
=
1
smN
(k
1
− m)
(k
1
− 1)
s(k
1
− 1)S
2
wst
h
1 + (s − 1)ρ
wst
i
.
Hence
(2.5) V (¯y
MSSM
) =
k
1
− m
mN
S
2
wst
h
1 + (s − 1)ρ
wst
i
.

194 Sat Gupta, Zaheen Khan and Javid Shabbir
3. MEAN, VARIANCE AND EFFICIENCY COMPARISON OF
MSSM FOR POPULATIONS EXHIBITING LINEAR TREND
Generally the efficiency of every new systematic sampling design is evalu-
ated for populations having linear trend. Therefore, consider the following linear
model for the hypothetical population
(3.1) Y
t
= α + βt, t = 1, 2, 3, ..., N,
where α and β respectively are the intercept and slope terms in the model.
3.1. Sample Mean under MSSM
¯y
MSSM
= α +
β
ms
m
X
i=1
s
X
j=1
n
r
i
+ (j − 1)k
1
o
, or
(3.2) ¯y
MSSM
= α +
β
m
n
m
X
i=1
r
i
+
m
2
(s − 1)k
1
o
.
(3.3) E (¯y
MSSM
) = α + β
(N + 1)
2
= µ.
V (¯y
MSSM
) = E {¯y
MSSM
− E(¯y
MSSM
)}
2
= β
2
E
h
1
m
m
X
i=1
r
i
−
(k
1
+ 1)
2
i
2
.
Hence
(3.4) V (¯y
MSSM
) = β
2
(k
1
+ 1)(k
1
− m)
12m
.
Note that m = 1 and k
1
= k in situations when MSSM is LSS; therefore
(3.5) V (¯y
MSSM
) = β
2
(k
2
− 1)
12
= V (¯y
LSS
) .
Similarly, m = n and k
1
= N in situations when MSSM is SRS, so
(3.6) V (¯y
MSSM
) = β
2
(N + 1)(N − n)
12n
= V (¯y
SRS
) .
The efficiency of MSSM with respect to SRS can be calculated as below:
(3.7) Efficiency =
V (¯y
SRS
)
V (¯y
MSSM
)
=
m(N + 1)(N − n)
(k
1
+ 1)(k
1
− m)n
=
(sk
1
+ 1)
(k
1
+ 1)
≥ 1,
as s ≥ 1. One can see that MSSM is always more efficient than SRS if s > 1 and
is equally efficient if s = 1.

Modified Systematic Sampling with Multiple Random Starts 195
4. ESTIMATION OF VARIANCE
Sampath and Ammani (2012) have considered LSS, Balanced Systematic
Sampling (BSS) proposed by Sethi (1965), and Modified Systematic Sampling
(MS) proposed by Singh et al. (1968) using multiple random starts. They have
derived excellent expressions of unbiased variance estimators and their variances
for these schemes. However, these schemes are not applicabl e if N 6= nk. Fortu-
nately, MSSM nicely handles this by producing unbiased variance estimator and
its variance for the case, where N 6= nk. Adopting the pro ce dure mentioned in
Sampath and Ammani (2012), we can get an unbiased variance estimator and its
variance in MSSM for the case where N 6= nk.
In MSSM, the probability that the i
th
unit will be included in the sam-
ple is just the probability of including the group containing the specific unit in
the sample. Hence, the first-order inclusion probability that corresponds to the
population unit with label i, is given by
π
i
=
m
k
1
=
ms
sk
1
=
n
N
, i = 1, 2, 3, ..., N.
In the second-order inclusion probabilities, the pairs of units may belong to
the same or the different groups. The pairs of units belong to the same group only
if the respective group is included in the sample. Thus, the second-order inclusion
probabilities for pairs of units belonging to the same group are equivale nt to the
first-order inclusion probabilities, i.e.,
π
ij
=
m
k
1
=
ms
sk
1
=
n
N
, i, j ∈ s
r
u
for some r
u
(r
u
= 1, 2, ..., k
1
).
On the other hand, pairs of units belonging to two different groups occurs
only when the corresponding pair of groups is included in the sample. Hence, the
second-order inclusion probability is given by
π
ij
=
m(m − 1)
k
1
(k
1
− 1)
, if i ∈ s
r
u
and j ∈ s
r
v
for some u 6= v.
Thus
π
ij
=
m(m − 1)
k
1
(k
1
− 1)
=
ms(ms − s)
sk
1
(sk
1
− s)
=
n(n − s)
N(N − s)
.
Since the second-order inclusion probabilities are p ositive for all pairs of
units in the population, an unbiased estimator of population variance can be
established. To accomplish this, the population variance
S
2
=
1
N − 1
N
X
i=1
(Y
i
− µ)
2

196 Sat Gupta, Zaheen Khan and Javid Shabbir
can be written as
S
2
=
1
2N(N − 1)
N
X
i=1
N
X
j=1
j6=i
(Y
i
− Y
j
)
2
.
By using second-order inclusion probabilities, an unbiased estimator of the pop-
ulation variance can be obtained as
ˆ
S
2
MSSM
=
1
2N(N − 1)
n
X
i=1
n
X
j=1
j6=i
(y
i
− y
j
)
2
π
ij
.
As n = ms, it means that there are m random sets each containing s units. There-
fore, taking r
u
(u = 1, 2, ...m) as the random start for the u
th
set, the expression
for
ˆ
S
2
MSSM
can be rewritten as:
ˆ
S
2
MSSM
=
1
2N(N − 1)
m
X
u=1
s
X
i=1
s
X
j=1
j6=i
(y
r
u
i
− y
r
u
j
)
2
π
ij
+
m
X
u=1
v=1
u6=v
s
X
i=1
s
X
j=1
(y
r
u
i
− y
r
v
j
)
2
π
ij
=
1
2N(N − 1)
N
n
m
X
u=1
s
X
i=1
s
X
j=1
j6=i
(y
r
u
i
− y
r
u
j
)
2
+
N(N − s)
n(n − s)
m
X
u=1
v=1
u6=v
s
X
i=1
s
X
j=1
(y
r
u
i
− y
r
v
j
)
2
=
1
2N(N − 1)
N
n
m
X
u=1
2s
s
X
i=1
(y
r
u
i
− ¯y
r
u
)
2
+
N(N − s)
n(n − s)
m
X
u=1
v=1
u6=v
s
X
i=1
s
X
j=1
(y
r
u
i
− ¯y
u
)
2
+ (y
r
v
j
− ¯y
r
v
)
2
+ (¯y
r
u
− ¯y
r
v
)
2
=
1
2N(N − 1)
N
n
m
X
u=1
n
2s
2
ˆσ
2
r
u
o
+
N(N − s)
n(n − s)
m
X
u=1
v=1
u6=v
n
s
2
ˆσ
2
r
u
+ s
2
ˆσ
2
r
v
+ s
2
(¯y
r
u
− ¯y
r
v
)
2
o
,
where ¯y
r
u
and ˆσ
2
r
u
=
1
s
s
X
i=1
(y
r
u
i
− ¯y
r
u
)
2
are the mean and variance of the u
th
group

Modified Systematic Sampling with Multiple Random Starts 197
(u = 1, 2, ..., m). Further,
ˆ
S
2
MSSM
=
1
2N(N − 1)
N
n
n
2s
2
m
X
u=1
ˆσ
2
r
u
o
+
N(N − s)
n(n − s)
n
2(m − 1)s
2
m
X
u=1
ˆσ
2
r
u
+ s
2
m
X
u=1
m
X
v=1
u6=v
(¯y
r
u
− ¯y
r
v
)
2
o
=
1
2N(N − 1)
N
n
n
2s
2
m
X
u=1
ˆσ
2
r
u
o
+
N(N − s)
n(n − s)
n
2(m − 1)s
2
m
X
u=1
ˆσ
2
r
u
+ s
2
2
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
o
=
s
2
ms(N − 1)
m
X
u=1
ˆσ
2
r
u
1 +
(N − s)
(ms − s)
(m − 1)
+
(N − s)
(ms − s)
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
.
Hence
(4.1)
ˆ
S
2
MSSM
=
1
(N − 1)
m
X
u=1
ˆσ
2
r
u
N
m
+
(N − s)
m(m − 1)
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
.
For simplicity, Equation (4.1) can be written as
ˆ
S
2
MSSM
=
1
(N − 1)
"
N
m
m
X
u=1
ˆσ
2
r
u
+
(N − s)
(m − 1)
m
X
u=1
(¯y
r
u
− ¯y
MSSM
)
2
#
.
The resulting estimator obtained in Equation (4.1) is an unbiased estimator of
population variance S
2
. It is mentioned in Section 2, if lcm of N and n is the
product of N and n, i.e., L = N × n, then MSSM be comes SRS.
Consequently, ˆσ
2
r
u
= 0(u = 1, 2, ..., m) and
ˆ
S
2
MSSM
=
ˆ
S
2
SRS
=
1
(n − 1)
n
X
i=1
(y
i
− ¯y)
2
,
which is a well-known unbiased estimator of S
2
in SRS without replacement.

198 Sat Gupta, Zaheen Khan and Javid Shabbir
4.1. Variance of
ˆ
S
2
MSSM
The variance of
ˆ
S
2
MSSM
is given by
(4.2)
V
ˆ
S
2
MSSM
=
1
m (N − 1)
2
"
N
2
(k
1
− m)
(k
1
− 1)
σ
2
0
+
(N − s)
2
k
1
(m − 1)
"
(m − 1)
(k
1
− 1)
−
(m − 2) (m − 3)
(k
1
− 2) (k
1
− 3)
µ
4
+
(k
1
− 3) − (m − 2) (k
1
+ 3)
(k
1
− 1)
2
+
(m − 2) (m − 3)
k
2
1
− 3
(k
1
− 1)
2
(k
1
− 2) (k
1
− 3)
µ
2
2
#
+ 2
N (N − s) (k
1
− m)
(k
1
− 1) (k
1
− 2)
k
1
X
r=1
ˆσ
2
r
¯y
r
−
¯
Y
2
− k
1
¯σ
2
µ
2
#
(see details in Appendix A).
Note that, if L = N, then MSSM becomes LSS and the above formula is not
valid in this case. Fortunately, in LSS, due to Gautschi (1957), the population is
divided into m
′
k groups of n/m
′
elements, and m
′
of these groups will randomly
be selected to get a sample of size n. Thus, one can easily modify the above
formula by just putting m = m
′
, k
1
= m
′
k and s = n/m
′
in Equation (A.9) and
get V
ˆ
S
2
LSS
as below:
(4.3)
V
ˆ
S
2
LSS
=
1
m
′
(N − 1)
2
"
N
2
m
′
(k − 1)
(m
′
k − 1)
σ
2
0
+
(m
′
N − n)
2
k
m
′
(m
′
− 1)
"
(m
′
− 1)
(m
′
k − 1)
−
(m
′
− 2) (m
′
− 3)
(m
′
k − 2) (m
′
k − 3)
µ
4
+
(m
′
k − 3) − (m
′
− 2) (m
′
k + 3)
(m
′
k − 1)
2
+
(m
′
− 2) (m
′
− 3)
m
′2
k
2
− 3
(m
′
k − 1)
2
(m
′
k − 2) (m
′
k − 3)
µ
2
2
#
+ 2
N (m
′
N − n) (k − 1)
(m
′
k − 1) (m
′
k − 2)
m
′
k
X
r=1
ˆσ
2
r
(¯y
r
− µ)
2
− m
′
k¯σ
2
µ
2
#
.
This is the general formula for the variance of unbiased variance estimator
with m
′
random starts for LSS. Further, one can also easily deduce the following

Modified Systematic Sampling with Multiple Random Starts 199
formula of V
ˆ
S
2
SRS
by putting k
1
= N , m = n and s = 1 in Equation (A.9):
(4.4)
V
ˆ
S
2
SRS
=
N
n (n − 1)
"
(n − 1)
(N − 1)
−
(n − 2) (n − 3)
(N − 2) (N − 3)
µ
4
+
(N − 3) − (n − 2) (N + 3)
(N − 1)
2
+
N
2
− 3
(n − 2) (n − 3)
(N − 1)
2
(N − 2) (N − 3)
µ
2
2
#
.
5. EFFICIENCY COMPARISON OF VARIANCE ESTIMATORS
In this section, we compare
ˆ
S
2
MSSM
with
ˆ
S
2
SRS
by using natural and sim-
ulated populations. Furthermore, this study is carried out for those choices of
sample sizes in which the condition “N < L < (N × n)” is satisfied. It has al-
ready been mentioned that MSSM becomes LSS when L = N. On the other
hand, MSSM becomes SRS when L = (N × n).
5.1. Natural Populations
In Population 1 (see Murthy, 1967, p. 131–132), the data on volume of tim-
ber of 176 forest strips have been considered. In this data, the volume of timber
has been arranged with respect to its length. In Population 2 (see Murthy, 1967,
p. 228), the data of output along with the fixed capital of 80 factories have been
considered. Here, output is arranged with respect to fixed capital. It is observed
that the data considered in Population 1 and Population 2 approximately follow
a linear trend. In this empirical study, the variances of
ˆ
S
2
MSSM
and
ˆ
S
2
SRS
are
computed for various sample sizes and efficiency is computed using the expression:
Efficiency =
V
ˆ
S
2
SRS
V
ˆ
S
2
MSSM
.
The population size N, sample size n, number of random starts m, number of
elements in each group s, the number of groups k
1
containing the N units of
the population and efficiency of MSSM over SRS are respectively presented in
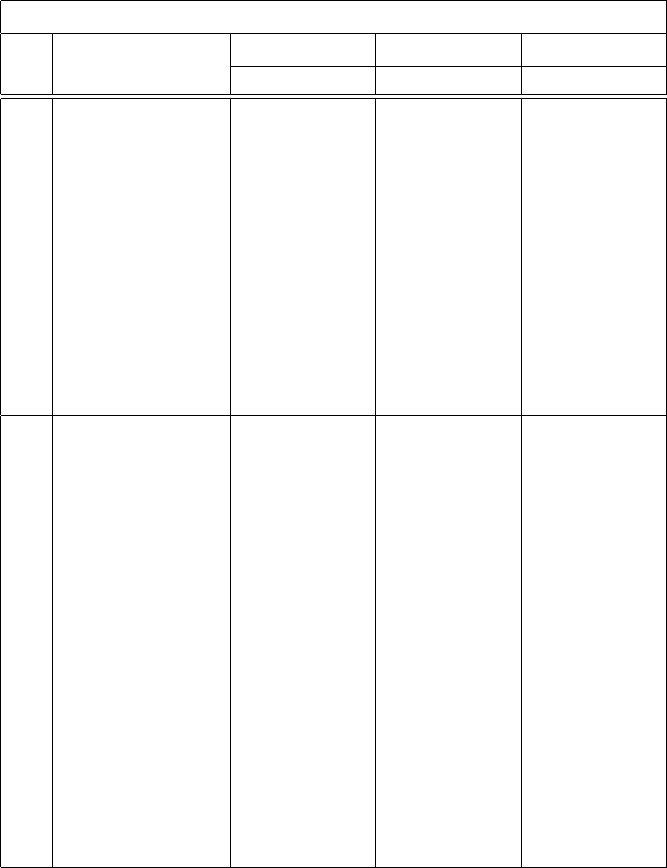
Columns 1 to 6 for Population 1 and Columns 7 to 12 for Population 2 in Table
2. From the efficiency comparison presented in Table 2, it has been observed
that MSSM is more efficient than SRS. Moreover, one can also see that as the
number of elements s in each group are increased, the efficiency of MSSM also
increases. Such increase in efficiency is due to the fact that in MSSM, the units

200 Sat Gupta, Zaheen Khan and Javid Shabbir
within the groups are arranged in a systematic pattern. So, more number of units
with systematic pattern will cause increase in efficiency.
Table 2: Efficiency comparison of
ˆ
S
2
M SSM
and
ˆ
S
2
SRS
in both natural populations.
Population 1 Population 2
N n m s k
1
Efficiency N n m s k
1
Efficiency
176
10 5 2 88 1.41
80
6 3 2 40 2.31
12 3 4 44 3.69 12 3 4 20 3.56
14 7 2 88 2.04 14 7 2 40 2.29
18 9 2 88 2.03 15 3 5 16 5.91
20 5 4 44 3.64 18 9 2 40 2.28
24 3 8 22 5.79 22 11 2 40 2.27
26 13 2 88 2.01 24 3 8 10 14.11
28 7 4 44 3.61 25 5 5 16 5.91
30 15 2 88 2.00 26 13 2 40 2.27
32 2 16 11 6.22 28 7 4 20 3.50
34 17 2 88 2.00 30 3 10 8 10.85
36 9 4 44 3.59 32 2 16 5 15.14
38 19 2 88 2.00 34 17 2 40 2.26
40 5 8 22 5.70 35 7 5 16 5.89
42 21 2 88 1.99 36 9 4 20 3.49
46 23 2 88 1.99 38 19 2 40 2.26
50 25 2 88 1.99
5.2. Simulated Populations
The simulation study, two populations of sizes 160 and 280 are generated
for the following distribution with variety of parameters by using R-packages:
(i) Uniform distribution: Here only three sets of the parametric values
are considered, i.e., (10, 20), (10, 30) and (10, 50).
(ii) Normal distribution: In this case, six sets of parametric values are
considered with means 20, 40 and 60 and standard deviations 5 and 8.
(iii) Gamma distribution: Eight sets of parametric values are considered
in this case. Here, 1, 3, 5 and 10 are considered as the values of scale
parameter with 2 and 4 as the values of shape parameter.
In each distribution, using each combination of the parametric values for each
choice of the sample size, each population with and without order is replicated
1000 times. V
ˆ
S
2
MSSM
and V
ˆ
S
2
SRS
are computed for each population (with
and without order) for the various choices of sample siz es. The average of 1000
values of the variances of
ˆ
S
2
MSSM
and
ˆ
S
2
SRS
is then computed for each population.

Modified Systematic Sampling with Multiple Random Starts 201
The efficiencies, Eff 1 and Eff 2 of MSSM compared to SRS are computed using
the following expressions:
Eff 1 =
Average
V
ˆ
S
2
SRSW OR
Average
V
ˆ
S
2
MSSM
without ordered p opulation
and
Eff 2 =
Average
V
ˆ
S
2
SRSW OR
Average
V
ˆ
S
2
MSSM
with ordered population.
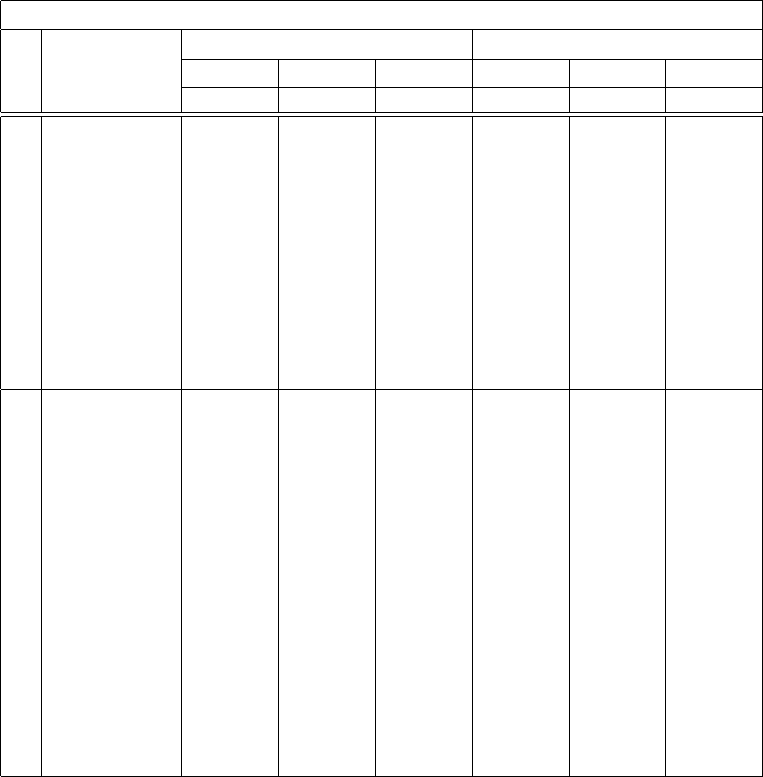
The efficiencies, Eff 1 and Eff 2 for Uniform distribution, Normal distribu-
tion and Gamma distribution are presented in Tables 3, 4 and 5 respectively.
It is observed that Eff 1 is approximately equal to 1 for almost all choices of
parametric values and sample sizes. This mean that MSSM and SRS are equally
efficient in case of random populations. Thus, for such populations, MSSM can be
preferred over SRS due to the qualities that there are no more issues of unbiased
estimation of population variance.
Furthermore, it is also observed from Tables 3, 4 and 5 that Eff 2 is greater
than 1 in all cases. It indicates that MSSM is more efficient than SRS in ordered
populations. The discussion of Eff 2 in Tables 3, 4 and 5 is as follows:
In Table 3, the efficiency (Eff 2) is not effected much by the different combi-
nations of parametric values of the uniform distribution and changes are caused
by the number of groups k
1
. It is also observed that MSSM is much more efficient
for the ordered populations of uniform distribution as compared to the normal
and gamma distributions.
In Table 4, the efficiency Eff 2 is also not much changed like uniform distri-
bution for different combinations of parametric values of the normal distribution.
However, Eff 2 is mainly changed due to the formation of number of groups k
1
of the population units in MSSM. Efficiency will increase with the decrease in
the number of groups k
1
, and it will decrease with the increase in the numb er of
groups k
1
.
In Table 5, the efficiency Eff 2 is effected by the number of groups k
1
along
with the shape parameter of the Gamma distribution. However, change in scale
parameter has no significant effect on efficiency of MSSM. Here also the efficiency
increases with decrease in the numb er of groups k
1
.
From the above discussion, it is obvious that MSSM performs better than
SRS for the p opulations that follow uniform and parabolic trends. However,
such populations must be ordered with certain characteristics. To know further
about the performance of MSSM, it would be interesting to study the variances
of
ˆ
S
2
MSSM
and
ˆ
S
2
SRS
in the presence of linear trend. This study has been carried
out in the following section.
202 Sat Gupta, Zaheen Khan and Javid Shabbir
Table 3: Efficiency of MSSM over SRS using uniform distribution.
Uniform Distribution
N n m s k
1
a = 10, b = 20 a = 10, b = 30 a = 10 , b = 50
Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2
160
12 3 4 40 0.94 24.17 0.94 24.67 0.94 24.33
14 7 2 80 1.00 5.99 0.99 6.04 0.98 6.05
15 3 5 32 0.95 39.72 0.96 38.39 0.95 39.85
18 9 2 80 0.99 6.19 0.99 6.16 1.00 6.15
22 11 2 80 1.00 6.17 1.00 6.26 1.00 6.25
24 3 8 20 0.94 91.20 0.95 90.56 0.98 89.22
25 5 5 32 0.99 44.66 0.99 44.24 0.98 45.01
26 13 2 80 1.00 6.30 1.00 6.37 1.00 6.26
28 7 4 40 0.99 29.47 1.00 30.36 0.99 28.90
30 3 10 16 0.98 125.89 0.98 125.98 0.96 120.79
34 17 2 80 1.00 6.33 1.00 6.50 1.00 6.44
35 7 5 32 1.00 43.94 0.99 46.98 0.99 45.59
36 9 4 40 0.99 30.19 1.00 30.60 0.99 30.23
38 19 2 80 1.00 6.44 1.00 6.45 0.99 6.37
280
12 3 4 70 0.94 28.07 0.94 28.44 0.93 28.48
15 3 5 56 0.94 47.65 0.94 47.37 0.94 47.68
16 2 8 35 0.89 102.47 0.89 104.25 0.90 103.83
18 9 2 140 0.99 6.41 0.99 6.50 0.99 6.51
22 11 2 140 0.99 6.61 0.99 6.48 1.00 6.60
24 3 8 35 0.96 123.18 0.96 121.88 0.96 124.69
25 5 5 56 0.98 55.48 0.98 56.05 0.99 54.97
26 13 2 140 0.99 6.74 0.99 6.77 1.00 6.62
30 3 10 28 0.96 189.18 0.97 182.58 0.97 184.39
32 4 8 35 0.97 135.94 0.98 131.74 0.99 134.95
34 17 2 140 1.00 6.75 1.00 6.88 1.00 6.84
36 9 4 70 0.99 38.04 1.00 36.47 0.99 36.59
38 19 2 140 1.00 6.82 1.00 6.85 1.00 6.83
42 3 14 20 0.99 292.91 0.98 320.06 0.96 310.45
44 11 4 70 1.00 38.00 0.99 37.56 1.00 37.28
45 9 5 56 1.00 61.45 1.00 60.35 1.00 59.46
46 23 2 140 1.00 7.02 1.00 6.86 1.00 6.95
48 6 8 35 0.99 144.63 0.99 148.64 1.01 141.89
49 7 7 40 1.00 111.72 1.00 118.32 1.00 114.09
50 5 10 28 0.99 195.80 0.99 199.00 0.99 207.92
Modified Systematic Sampling with Multiple Random Starts 203
Table 4: Efficiency of MSSM over SRS using normal distribution.
Normal distribution
σ = 5 σ = 10
N n m s k
1
µ = 20 µ = 40 µ = 60 µ = 20 µ = 40 µ = 60
Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2 Eff1 Eff 2 Eff 1 Eff 2
160
12 3 4 40 0.97 3.33 0.97 3.34 0.98 3.35 0.96 3.34 0.97 3.31 0.97 3.28
14 7 2 80 0.99 1.79 1.00 1.80 1.00 1.79 1.01 1.79 0.99 1.80 1.00 1.80
15 3 5 32 0.98 4.01 0.97 4.11 0.98 4.11 0.97 4.00 0.97 4.02 0.99 4.06
18 9 2 80 1.00 1.78 0.99 1.78 0.99 1.80 0.99 1.79 1.00 1.78 1.00 1.79
22 11 2 80 1.00 1.79 0.99 1.80 0.99 1.78 1.00 1.79 1.00 1.78 0.99 1.77
24 3 8 20 0.98 6.04 0.98 6.33 0.98 6.19 0.98 6.23 1.00 6.19 0.97 6.16
25 5 5 32 0.99 3.98 0.99 4.04 0.99 4.05 0.98 4.06 0.99 4.07 1.00 4.03
26 13 2 80 1.00 1.79 1.00 1.79 1.00 1.77 1.00 1.78 1.00 1.79 0.99 1.79
28 7 4 40 0.99 3.30 0.99 3.28 1.00 3.27 1.00 3.32 0.99 3.30 0.99 3.32
30 3 10 16 0.98 7.49 0.98 7.67 0.99 7.72 0.99 7.54 1.00 7.41 0.99 7.77
34 17 2 80 1.00 1.78 1.00 1.78 1.00 1.79 0.99 1.79 1.00 1.79 1.00 1.78
35 7 5 32 1.00 4.00 1.00 4.03 0.99 4.03 0.99 4.04 0.99 3.99 1.01 4.01
36 9 4 40 1.00 3.34 1.00 3.25 1.00 3.28 1.01 3.32 0.99 3.30 1.00 3.29
38 19 2 80 0.99 1.81 1.00 1.79 1.00 1.77 1.00 1.78 1.00 1.78 1.00 1.79
280
12 3 4 70 0.96 3.34 0.97 3.31 0.96 3.33 0.97 3.33 0.97 3.35 0.97 3.33
15 3 5 56 0.96 4.12 0.98 4.03 0.97 4.05 0.97 4.14 0.99 4.09 0.97 4.01
16 2 8 35 0.95 6.30 0.95 6.16 0.94 6.26 0.95 6.31 0.95 6.29 0.94 6.35
18 9 2 140 1.00 1.79 0.99 1.79 1.00 1.80 0.99 1.79 1.00 1.79 1.00 1.79
22 11 2 140 1.00 1.79 1.00 1.78 1.00 1.80 0.99 1.79 1.00 1.80 1.00 1.80
24 3 8 35 0.98 6.17 0.99 6.35 0.99 6.06 0.98 6.25 0.98 6.14 0.98 6.26
25 5 5 56 0.99 4.01 1.00 4.11 1.00 4.05 1.00 4.07 0.99 4.04 0.99 4.02
26 13 2 140 1.00 1.80 0.99 1.79 1.00 1.80 1.00 1.78 1.00 1.81 1.00 1.79
30 3 10 28 0.98 7.53 0.98 7.73 0.99 7.72 0.99 7.98 1.00 7.78 0.99 7.71
32 4 8 35 0.99 6.17 1.00 6.38 1.00 6.16 1.00 6.35 0.99 6.16 0.99 6.37
34 17 2 140 1.00 1.78 1.00 1.79 0.99 1.78 1.00 1.78 1.00 1.79 1.00 1.79
36 9 4 70 1.00 3.33 0.99 3.33 1.00 3.33 0.99 3.28 1.00 3.34 0.99 3.38
38 19 2 140 1.00 1.78 1.00 1.78 1.00 1.79 1.00 1.79 1.00 1.79 1.00 1.80
42 3 14 20 0.98 10.32 0.98 10.12 0.99 10.35 1.00 10.55 1.00 10.36 0.99 10.53
44 11 4 70 1.00 3.30 1.00 3.31 1.00 3.36 1.00 3.28 0.99 3.30 1.00 3.30
45 9 5 56 0.99 4.07 0.99 4.08 1.01 4.01 1.00 4.07 0.99 4.03 1.00 4.10
46 23 2 140 1.00 1.78 1.00 1.79 0.99 1.79 1.00 1.79 1.00 1.79 0.99 1.78
48 6 8 35 0.99 6.22 0.98 6.24 1.00 6.16 0.99 6.19 1.01 6.39 1.00 6.21
49 7 7 40 1.00 5.66 1.00 5.52 1.00 5.49 0.99 5.49 0.99 5.48 1.00 5.50
50 5 10 28 1.00 7.89 0.99 7.54 1.00 7.82 0.99 7.59 0.99 7.54 1.01 7.72
204 Sat Gupta, Zaheen Khan and Javid Shabbir
Table 5: Efficiency of MSSM over SRS using gamma distribution.
Gamma distribution
shape = 2 shape = 4
N n m s k
1
scale =1 scale =3 scale =5 scale = 10 scale =1 scale =3 scale =5 scale = 10
Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2 Eff 1 Eff 2
160
12 3 4 40 1.00 1.50 0.98 1.48 0.99 1.45 0.98 1.42 0.98 1.77 0.99 1.75 0.97 1.77 0.99 1.74
14 7 2 80 0.99 1.21 0.99 1.20 1.00 1.21 1.00 1.21 1.00 1.34 0.99 1.34 1.00 1.33 1.00 1.34
15 3 5 32 1.01 1.54 0.98 1.57 0.99 1.54 1.00 1.59 0.99 1.89 1.00 1.89 0.97 1.90 0.98 1.89
18 9 2 80 0.99 1.21 0.99 1.20 1.00 1.21 1.00 1.20 1.00 1.33 1.00 1.34 1.00 1.33 1.00 1.34
22 11 2 80 1.01 1.20 1.01 1.21 1.00 1.21 1.00 1.20 0.99 1.32 0.99 1.33 1.00 1.32 1.00 1.33
24 3 8 20 0.99 1.81 1.00 1.79 1.00 1.77 1.00 1.86 0.99 2.32 1.00 2.27 1.00 2.25 1.00 2.26
25 5 5 32 1.01 1.55 0.99 1.57 1.00 1.53 0.99 1.56 0.99 1.92 1.00 1.87 0.99 1.89 1.00 1.87
26 13 2 80 1.00 1.20 1.00 1.19 1.00 1.20 1.00 1.20 0.99 1.33 1.00 1.32 1.00 1.33 1.00 1.32
28 7 4 40 1.00 1.45 1.00 1.44 1.00 1.46 0.99 1.44 0.99 1.76 1.00 1.72 1.00 1.73 0.99 1.72
30 3 10 16 0.99 1.91 1.00 1.98 1.00 1.90 0.98 1.98 0.98 2.53 0.98 2.44 0.99 2.51 1.01 2.44
34 17 2 80 1.00 1.20 1.00 1.21 1.00 1.20 1.00 1.19 1.00 1.33 1.00 1.33 1.00 1.33 1.00 1.31
35 7 5 32 0.99 1.55 0.99 1.56 1.00 1.53 1.01 1.56 1.00 1.86 1.00 1.89 0.98 1.89 1.00 1.89
36 9 4 40 0.99 1.43 1.00 1.45 1.00 1.47 1.01 1.45 1.00 1.75 0.99 1.76 1.00 1.76 0.99 1.76
38 19 2 80 0.99 1.20 1.00 1.21 0.99 1.20 1.00 1.20 1.01 1.32 1.00 1.32 1.00 1.32 1.00 1.33
280
12 3 4 70 0.98 1.48 0.99 1.46 0.99 1.46 0.99 1.46 0.98 1.76 0.98 1.78 0.99 1.76 0.99 1.76
15 3 5 56 0.99 1.57 0.98 1.58 0.99 1.56 1.00 1.57 0.98 1.92 0.98 1.95 0.99 1.89 0.99 1.94
16 2 8 35 0.99 1.82 0.98 1.80 0.98 1.77 0.97 1.85 0.98 2.29 0.98 2.26 0.98 2.32 0.96 2.29
18 9 2 140 1.00 1.21 1.00 1.20 1.00 1.21 1.00 1.20 1.00 1.33 1.00 1.33 1.00 1.34 1.00 1.34
22 11 2 140 1.00 1.21 0.99 1.21 1.00 1.20 1.00 1.21 1.00 1.33 1.00 1.32 1.00 1.32 1.00 1.34
24 3 8 35 0.98 1.84 0.99 1.79 0.99 1.82 1.00 1.82 0.99 2.31 0.98 2.27 0.99 2.29 0.99 2.24
25 5 5 56 0.99 1.55 1.01 1.56 1.00 1.53 1.00 1.55 0.99 1.92 1.00 1.88 1.00 1.89 1.00 1.87
26 13 2 140 1.00 1.20 0.99 1.20 1.00 1.20 1.00 1.21 1.00 1.33 1.00 1.32 1.00 1.32 1.00 1.32
30 3 10 28 1.00 1.93 0.99 1.91 0.99 1.89 1.00 1.96 0.99 2.48 0.98 2.53 0.98 2.52 0.99 2.47
32 4 8 35 1.00 1.81 0.99 1.79 1.00 1.80 1.00 1.80 1.00 2.24 1.00 2.27 1.01 2.28 0.98 2.26
34 17 2 140 1.00 1.20 1.00 1.20 1.00 1.21 1.00 1.19 1.00 1.33 1.00 1.33 1.00 1.33 1.00 1.32
36 9 4 70 0.99 1.44 1.00 1.44 1.00 1.44 0.99 1.44 0.99 1.71 1.00 1.75 1.00 1.75 1.00 1.70
38 19 2 140 1.00 1.20 1.00 1.20 1.00 1.19 1.00 1.20 1.00 1.34 1.00 1.32 1.01 1.32 1.00 1.33
42 3 14 20 0.97 2.13 0.98 2.19 0.99 2.19 0.98 2.13 1.00 2.81 0.98 2.93 1.00 2.83 0.99 2.80
44 11 4 70 1.00 1.46 1.00 1.46 1.00 1.47 0.99 1.46 0.99 1.71 1.00 1.74 1.00 1.72 1.01 1.74
45 9 5 56 1.01 1.56 1.00 1.55 1.00 1.54 1.00 1.53 0.99 1.90 1.01 1.91 0.99 1.88 0.98 1.90
46 23 2 140 1.00 1.20 1.00 1.19 1.00 1.20 1.00 1.20 1.00 1.33 1.00 1.33 1.00 1.32 1.00 1.32
48 6 8 35 1.01 1.79 1.01 1.82 0.98 1.76 1.01 1.78 1.00 2.27 1.00 2.30 1.00 2.29 1.00 2.26
49 7 7 40 1.00 1.72 0.99 1.70 0.99 1.70 0.99 1.74 1.00 2.13 1.00 2.16 0.99 2.11 1.00 2.12
50 5 10 28 1.00 1.92 0.99 1.96 1.00 1.96 0.98 1.94 1.01 2.47 0.99 2.48 1.00 2.46 1.00 2.42

Modified Systematic Sampling with Multiple Random Starts 205
6. VARIANCE OF
ˆ
S
2
MSSM
IN THE PRESENCE OF LINEAR TREND
The variance of
ˆ
S
2
MSSM
under the linear Model (3.1) is given by
(6.1)
V
ˆ
S
2
MSSM
=
β
4
k
2
1
− 1
m (N − 1)
2
(N − s)
2
k
1
(m − 1)
×
"
3k
2
1
− 7
240
(m − 1)
(k
1
− 1)
−
(m − 2) (m − 3)
(k
1
− 2) (k
1
− 3)
+
1
144
k
2
1
− 1
×
(k
1
− 3) − (m − 2) (k
1
+ 3)
(k
1
− 1)
2
(m − 2) (m − 3)
k
2
1
− 3
(k
1
− 1)
2
(k
1
− 2) (k
1
− 3)
#
(see details in Appendix B).
Substituting m = n, s = 1 and k
1
= N in (B.7), the variance of
ˆ
S
2
SRS
can
be obtained in the presence of linear trend, i.e.,
(6.2)
V
ˆ
S
2
SRS
=
β
4
N
2
− 1
N
n(n − 1)
"
3N
2
− 7
240
(n − 1)
(N − 1)
−
(n − 2) (n − 3)
(N − 2) (N − 3)
+
1
144
N
2
− 1
(N − 3) − (n − 2) (N + 3)
(N − 1)
2
+
(n − 2) (n − 3)
N
2
− 3
(N − 1)
2
(N − 2) (N − 3)
#
.
Similarly, substituting m = m
′
, k
1
= m
′
k and s = n/m
′
in Equation (B.7), one
can get the following formula of variance of unbiased variance estimator with m
′
random starts for LSS in the presence of linear trend.
(6.3)
V
ˆ
S
2
LSS
=
β
4
m
′2
k
2
− 1
(N − 1)
2
(m
′
N − n)
2
k
m
′2
(m
′
− 1)
×
"
3m
′2
k
2
− 7
240
(m
′
− 1)
(m
′
k − 1)
−
(m
′
− 2) (m
′
− 3)
(m
′
k − 2) (m
′
k − 3)
+
1
144
m
′2
k
2
− 1
(m
′
k − 3) − (m
′
− 2) (m
′
k + 3)
(m
′
k − 1)
2
+
(m
′
− 2) (m
′
− 3)
m
′2
k
2
− 3
(m
′
k − 1)
2
(m
′
k − 2) (m
′
k − 3)
#
.
206 Sat Gupta, Zaheen Khan and Javid Shabbir
6.1. Efficiency Comparison of
ˆ
S
2
MSSM
and
ˆ
S
2
SRS
in the Presence of
Linear Trend
Due to complicated expressions given in Equation (B.7) and (6.2), the-
oretical comparison of
ˆ
S
2
MSSM
and
ˆ
S
2
SRS
is not easy. Therefore, a numerical
comparison is carried out by considering the linear Mo del (3.1) and results are
presented in Table 6.
Table 6: Efficiency of MSSM over SRS using linear model.
N n m s k
1
Efficiency N n m s k
1
Efficiency
160
12 3 4 40 34.76
280
12 3 4 70 34.81
14 7 2 80 6.72 15 3 5 56 65.24
15 3 5 32 65.13 16 2 8 35 169.87
18 9 2 80 6.98 18 9 2 140 6.98
22 11 2 80 7.15 22 11 2 140 7.15
24 3 8 20 250.30 24 3 8 35 250.80
25 5 5 32 84.36 25 5 5 56 84.56
26 13 2 80 7.27 26 13 2 140 7.27
28 7 4 40 49.07 30 3 10 28 479.29
30 3 10 16 478.57 32 4 8 35 299.77
34 17 2 80 7.42 34 17 2 140 7.43
35 7 5 32 94.01 36 9 4 70 52.04
36 9 4 40 51.92 38 19 2 140 7.49
38 19 2 80 7.48 42 3 14 20 1282.26
44 11 4 70 53.96
45 9 5 56 100.13
46 23 2 140 7.57
48 6 8 35 356.73
49 7 7 40 252.94
50 5 10 28 641.04
In Table 6, one can easily see that the lower the number of groups k
1
, the
higher is the efficiency, and v ice versa. Note that different choices of α and β do
not have any effect on the efficiencies as the parameters α and β will drop out
from variance and efficiency expressions respectively.

Modified Systematic Sampling with Multiple Random Starts 207
7. CONCLUSION
The proposed MSSM design is based on adjusting the population units
in groups. Thus, except the two extreme cases of this design, MSSM is neither
completely systematic nor random but displaying the amalgamation of systematic
and simple random sampling. In the two extreme cases, one of them becomes LSS
and other SRS. The MSSM makes it possible to develop the modified expressions
of all the results that relates to the LSS. A few such modifications are reported
in Sections 2 and 3. A theoretical efficiency comparison of MSSM and SRS using
the variances of mean in the presence of l inear trend is c arried out and is shown
in Equation (3.1). This comparison clearly indicates that MSSM is more efficient
than SRS.
In this study, population variance is unbiasedly estimated in MSSM for all
possible combinations of N and n. An explicit expression for variance of unbiased
variance estimator is also obtained in the proposed design. Moreover, it enables
us to deduce the expressions for variance of unbiased variance estimator for LSS
and SRS. Due to the complex nature of these expressions, theoretical comparison
is not an easy task. Therefore, numerical comparison of MSSM and SRS is carried
out in Sections 5 and 6. This numerical efficiency comparison is done for natural
population, simulated population and li near mo del having a perfect linear trend.
The results show that if populations (with linear or parabolic trend) are arranged
with certain characteristics then MSSM is more efficient than SRS. However, in
simulated p opulations, MSSM is almost equally efficient to SRS as units are not
arranged in specific order. In this case, one can benefit from MSSM due to
its simplicity and economical status. Furthermore, the findings reveal that the
efficiency of MSSM is quite high for those combinations of N and n in which all
population units are arranged in minimum numb er of groups.

208 Sat Gupta, Zaheen Khan and Javid Shabbir
APPENDIX A — Variance of
ˆ
S
2
MSSM
The variance of
ˆ
S
2
MSSM
can be written as
(A.1)
V
ˆ
S
2
MSSM
=
1
(N − 1)
2
N
m
2
V
m
X
u=1
ˆσ
2
r
u
+
(N − s)
m(m − 1)
2
V
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
+ 2
N
m
(N − s)
m(m − 1)
Cov
m
X
u=1
ˆσ
2
r
u
,
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
.
Note that
V
m
X
u=1
ˆσ
2
r
u
=
m
X
u=1
V
ˆσ
2
r
u
+
m
X
u=1
m
X
v=1
v6=u
Cov
ˆσ
2
r
u
, ˆσ
2
r
v
,
where
V (ˆσ
2
r
u
) =
1
k
1
k
1
X
u=1
ˆσ
2
r
u
− ¯σ
2
2
=
1
k
1
k
1
X
r=1
ˆσ
2
r
− ¯σ
2
2
= σ
2
0
(say)
such that
¯σ
2
=
1
k
1
k
1
X
u=1
ˆσ
2
r
u
=
1
k
1
k
1
X
r=1
ˆσ
2
r
and Cov
ˆσ
2
r
u
, ˆσ
2
r
v
= −
σ
2
0
(k
1
− 1)
.
Thus
(A.2) V
m
X
u=1
ˆσ
2
r
u
= mσ
2
0
k
1
− m
k
1
− 1
.
Now consider
V
h
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
i
=(A.3)
=
m−1
X
u=1
m
X
v=u+1
V
n
(¯y
r
u
− ¯y
r
v
)
2
o
+ 2
"
m
X
u=1
m
X
v=1
v6=u
m
X
u
′
=1
u
′
6=u,v
Cov
n
(¯y
r
u
− ¯y
r
v
)
2
,
¯y
r
u
− ¯y
r
u
′
2
o
+
m
X
u=1
m
X
v=1
v6=u
m
X
u
′
=1
u
′
6=u,v
m
X
v
′
=1
v
′
6=u,v,u
′
Cov
n
(¯y
r
u
− ¯y
r
v
)
2
,
¯y
r
u
′
− ¯y
r
v
′
2
o
#
,
Modified Systematic Sampling with Multiple Random Starts 209
where
(A.4) V (¯y
r
u
− ¯y
r
v
)
2
=
2k
1
(k
1
− 1)
µ
4
+
k
1
− 3
(k
1
− 1)
µ
2
2
,
such that
µ
2
=
1
k
1
k
1
X
u=1
(¯y
r
u
− µ)
2
=
1
k
1
k
1
X
r=1
(¯y
r
− µ)
2
and µ
4
=
1
k
1
k
1
X
r=1
(¯y
r
− µ)
4
.
(A.5) Cov
n
(¯y
r
u
− ¯y
r
v
)
2
,
¯y
r
u
− ¯y
r
u
′
2
o
=
k
1
(k
1
− 1)
µ
4
−
k
1
+ 3
(k
1
− 1)
µ
2
2
.
(A.6)
Cov
n
(¯y
r
u
− ¯y
r
v
)
2
,
¯y
r
u
′
− ¯y
r
v
′
2
o
=
−4k
1
(k
1
− 2) (k
1
− 3)
"
µ
4
−
k
2
1
− 3
(k
1
− 1)
2
µ
2
2
#
.
Putting (A.4), (A.5) and (A.6) in (A.3), we have
V
"
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
#
=
m
2
"
2k
1
(k
1
− 1)
µ
4
+
k
1
− 3
(k
1
− 1)
µ
2
2
#
+ 2
"
m
m − 1
2
k
1
(k
1
− 1)
µ
4
−
k
1
+ 3
(k
1
− 1)
µ
2
2
+
(
m(m−1)
2
2
− m
m − 1
2
)
×
−4k
1
(k
1
− 2) (k
1
− 3)
µ
4
−
k
2
1
− 3
(k
1
− 1)
2
µ
2
2
#
,
or
(A.7)
V
"
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
#
= m (m − 1) k
1
"
(m − 1)
(k
1
− 1)
−
(m − 2) (m − 3)
(k
1
− 2) (k
1
− 3)
µ
4
+
(k
1
− 3) − (m − 2) (k
1
+ 3)
(k
1
− 1)
2
+
(m − 2) (m − 3)
k
2
1
− 3
(k
1
− 1)
2
(k
1
− 2) (k
1
− 3)
µ
2
2
#
.
Also consider
Cov
m
X
u=1
ˆσ
2
r
u
,
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
=
= E
m
X
u=1
ˆσ
2
r
u
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
− E
m
X
u=1
ˆσ
2
r
u
E
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
,

210 Sat Gupta, Zaheen Khan and Javid Shabbir
where
E
m
X
u=1
ˆσ
2
r
u
=
m
X
u=1
E
ˆσ
2
r
u
= m
1
k
1
k
1
X
u=1
ˆσ
2
r
u
= m
1
k
1
k
1
X
r=1
ˆσ
2
r
= m ¯σ
2
,
E
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
=
m−1
X
u=1
m
X
v=u+1
E (¯y
r
u
− ¯y
r
v
)
2
=
m
2
2k
1
(k
1
− 1)
µ
2
and
E
m
X
u=1
ˆσ
2
r
u
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
=
m (m −1)
(k
1
− 1)
1 +
(m − 2) (k
1
− 1)
(k
1
− 2)
k
1
¯σ
2
µ
2
+
1 −
(m − 2)
(k
1
− 2)
k
1
X
r=1
ˆσ
2
r
(¯y
r
− µ)
2
,
or
(A.8)
Cov
(
m
X
u=1
ˆσ
2
r
u
,
m−1
X
u=1
m
X
v=u+1
(¯y
r
u
− ¯y
r
v
)
2
)
=
=
m (m − 1) (k
1
− m)
(k
1
− 1) (k
1
− 2)
(
k
1
X
r=1
ˆσ
2
r
(¯y
r
− µ)
2
− k
1
¯σ
2
µ
2
)
.
Putting (A.1), (A.7) and (A.8) in (A.1) and then simplifying, we have
(A.9)
V
ˆ
S
2
MSSM
=
1
m (N − 1)
2
"
N
2
(k
1
− m)
(k
1
− 1)
σ
2
0
+
(N − s)
2
k
1
(m − 1)
×
"
(m − 1)
(k
1
− 1)
−
(m − 2) (m − 3)
(k
1
− 2) (k
1
− 3)
µ
4
+
(k
1
− 3) − (m − 2) (k
1
+ 3)
(k
1
− 1)
2
+
(m − 2) (m − 3)
k
2
1
− 3
(k
1
− 1)
2
(k
1
− 2) (k
1
− 3)
µ
2
2
#
+ 2
N (N − s) (k
1
− m)
(k
1
− 1) (k
1
− 2)
k
1
X
r=1
ˆσ
2
r
¯y
r
−
¯
Y
2
− k
1
¯σ
2
µ
2
#
.

Modified Systematic Sampling with Multiple Random Starts 211
APPENDIX B — Variance of
ˆ
S
2
MSSM
Assuming the linear Model (3.1), the mean of the r
th
(r = 1, 2, ..., k
1
) group
can be written as
¯y
r
=
1
s
s
X
i=1
n
α + β
r + (i − 1)k
1
o
,
(B.1) ¯y
r
= α + β
r +
1
2
(s − 1)k
1
,
(B.2)
ˆσ
2
r
=
1
s
s
X
i=1
α + β
r + (i − 1)k
1
− α − β
r +
1
2
(s − 1)k
1
2
=
1
s
s
X
i=1
β(i − 1)k
1
− β
1
2
(s − 1)k
1
2
=
1
12
β
2
k
2
1
(s
2
− 1),
(B.3) ¯σ
2
r
=
1
12
β
2
k
2
1
(s
2
− 1),
(B.4) σ
2
0
= 0,
(B.5) µ
2
=
1
k
1
k
1
X
r=1
(¯y
r
− µ)
2
=
β
2
12
k
2
1
− 1
and
(B.6) µ
4
=
1
k
1
k
1
X
r=1
(¯y
r
− µ)
4
= β
4
k
4
1
80
−
k
2
1
24
+
7
240
,
where
µ = α + β
N + 1
2
.
Putting Equations (B.1)–(B.6) in (A.9), we have
(B.7)
V
ˆ
S
2
MSSM
=
β
4
k
2
1
− 1
m (N − 1)
2
(N − s)
2
k
1
(m − 1)
×
"
3k
2
1
− 7
240
(m − 1)
(k
1
− 1)
−
(m − 2) (m − 3)
(k
1
− 2) (k
1
− 3)
+
1
144
k
2
1
− 1
×
(k
1
− 3) − (m − 2) (k
1
+ 3)
(k
1
− 1)
2
(m − 2) (m − 3)
k
2
1
− 3
(k
1
− 1)
2
(k
1
− 2) (k
1
− 3)
#
.

212 Sat Gupta, Zaheen Khan and Javid Shabbir
ACKNOWLEDGMENTS
The authors offer their sincere thanks to the two reviewers for their careful
reading of the paper and their helpful suggestions.
REFERENCES
[1] Chang, H.J. and Huang, K.C. (2000). Remainder linear systematic sampling,
Sankhya, 62(B), 249–256.
[2] Gautschi, W. (1957). Some remarks on systematic sampling, The Annals of
Mathematical Statistics, 28(2), 385–394.
[3] Khan, Z.; Shabbir, J. and Gupta, S.N. (2013). A new sampling design for sys-
tematic sampling, Communications in Statistics — Theory and Methods, 42(18),
3359–3370.
[4] Murthy, M.N. (1967). Sampling Theory and Methods, Statistical Publishing
Society, Calcutta, India.
[5] Naidoo, L.R.; North, D.; Zewotir, T. and Arnab, R. (2016). Multiple-
start balanced modified systematic sampling in the presence of linear trend,
Communicat ions in Statistics — Theory and Methods, 45(14), 4307–4324.
[6] Sampath, S. (2009). Finite population variance estimation under lss with mul-
tiple random starts, Communication in Statistics — Theory and Methods, 38,
3596–3607.
[7] Sampath, S. and Ammani, S. (2012). Finite-p opulation variance estimation
under systematic sampling schemes with multiple random starts, Journal of
Statistical Computation and Simulation, 82(8), 1207–1221.
[8] Sethi, V.K. (1965). On optimum paring of units, Sankhya, 27(B), 315–320.
[9] Singh, D.; Jindal, K.K. and Garg, J.N. (1968). On modified systematic
sampling, Biometrika, 55, 541–546.
[10] Subramani, J. and Gupta, S.N. (2014). Generalized modified linear system-
atic sampling scheme, Hacettepe Journal of Mathematics and Statistics, 43(3),
529–542.
